CASE 8: FORMATION OF TORUS-UNSTABLE FLUX ROPES

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Animation 1

Animation 2

Figure 6

Animation 3

It is now widely accepted that solar eruptions are due to a violent destabilization of previously energized coronal magnetic fields (cf. also Case 6). However, the detailed mechanisms which bring a system into an eruptive stage, and which eventually drive the eruption, are not yet fully understood. In order to clarify the physical mechanisms that form a three-dimensional coronal flux rope and later cause its eruption, we present here a simulation of an initially bipolar, current-free, and asymmetric coronal magnetic field that evolves in response to simultaneous sub-Alfvénic annular vortex motions and to slow diffusion of the three magnetic field components, which are both prescribed at a line-tied photospheric boundary.

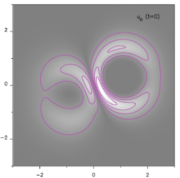
During the simulation the magnetic field evolves driven by the imposed sub-Alfvénic vortical motions at the photosphere (see Figure 1), and by diffusion (at and above the photosphere, see numerical details). The first stage of the evolution of the magnetic field is a quasi-static, long energy-storaging phase, where the magnetic field is stressed primarily along the polarity inversion line (PIL, see Figure 2). In this phase, lasting until approximately t=120 t_A, a stable flux rope is formed above the PIL (see Figure 3 and the first part of Animation 1; the Alfvén time t_A is the characteristic timescale of magnetic disturbances, see numerical details).

The flux rope formation has two consecutive, topologycally distinct phases. First, a bald patch (BP) is initially formed from the sheared arcade field lines by the combined effects of rotation and photospheric diffusion. A BP is a location along the PIL where coronal field lines touch tangentially the photosphere (see the left panel in Figure 4), and here currents can easily form as a consequence of plasma shearing flows. Arcade-type of field lines can then reconnect at the BP (flux cancellation) into longer field lines forming the flux rope (similar to the classical tether-cutting model of Sturrock (1989), but essentially due to photospheric diffusion). The BP is formed approximately at t=22 t_A, grows until t=70 t_A, and then rapidly disappears at t= 76 t_A.

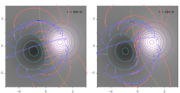
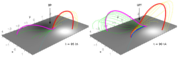
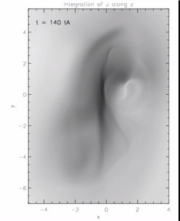
At this point the second phase of the flux rope formation starts with the appearance of a quasi-separatrix layer (QSL) rooted at the original position of the BP (see right panel in Figure 4, and Case 7 for a definition of QSLs). Since QSLs are locations of strong gradients in field-lines' connectivity, again current layers are formed which allow for reconnection to take place, increasing the flux within the rope. In particular, a coronal hyperbolic flux tube (HFT; see Titov et al. (2002)) exists within the core of our flux rope related QSL (see the right panel in Figure 4). The HFT is the generalization of a 2.5D X-point or a 3D separator. The middle part of the HFT is located above the photospheric plane, where the red/yellow and pink/green systems of field lines converge around the blue arcade. At t=100 t_A, the electric currents within the HFT start to develop in an elongated (vertical) layer, in which 3D finite-B reconnection (as opposed to null point reconnection) takes place. In the HFT, this naturally results in slipping and slip-running reconnection, which manifest as sub- and super-Alfvénic field line slipping motions, respectively (as identified in Aulanier et al. (2006) and (2007)). Slip-running reconnection starts from t=76 t_A, when the HFT forms. However, the rate at which field lines reconnect through the HFT, as well as the norm of the current density within it, significantly increase around t=100 t_A, once the vertical current layer has developed. Since it occurs in the corona, this reconnection is more similar to the standard tether-cutting model, forming also small sheared arcades below the flux rope (see the blue field line at t=90 t_A in Figure 4, right panel). Finally, in both phases of the energy-storage stage the flux rope is found to be stable (although slowly rising). This implies that even though tether-cutting reconnection can help feeding a flux rope from the flux of its surrounding sheared arcade, it does not lead to its eruption.

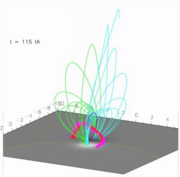
During the energy-storage phase, the flux rope rises quasi-statically with a velocity that is few percent of the initial Alfvén speed. Figure 5 and the second part of Animation 1 show that this phase is followed by an energy-release stage of the evolution, characterized by a fast acceleration and expansion of the rope and of its overlying arcade, up to heights which are much larger than the corresponding initial values (eruption). The analysis of the conversion of magnetic into kinetic energy shows that the energy-release phase starts gradually around around t=100 t_A, is in full development from t=120 t_A onwards, and saturates to a constant velocity (of about 0.4 c_A) at t=150 t_A. Once the system has sufficiently expanded, both the arcade field lines overlying the flux rope (Figures 5) and the coronal electric current densities display a wide inverse tear drop shape, which is typical for CMEs observed above the solar limb. The asymmetry in the erupting magnetic field that is evident in Animation 1 is related to the asymmetry in the initial potential field.

Studying the energetics and dynamics of the system (complemented by additional numerical tests, see Aulanier et al. (2010) for more details), we can exclude that the eruption is triggered by BP reconnection, tether-cutting reconnection, or weakening of the ovelying field due to photospheric diffusion (flux disappearance). These effects are all present and play a role in the dynamics of the system, but they either happen too early or are too weak to be responsible for the triggering of the eruption. On the other hand, at the time when the eruption is in full development (t∼120 t_A), the flux rope has reached a height where the ambient field drops too fast to be able to stabilize the current channel. The flux rope eruption can be therefore described in terms of the loss of stability of a toroidal current (previously developed during a long energy storage stage) which has eventually reached the altitude where the magnetic field decreases sufficiently fast with height for the torus instability to develop (Bateman (1978); Kliem et al. (2006)).

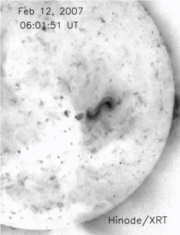
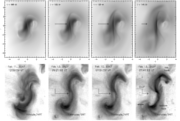
We used the described simulation to interpret the eruption of a sigmoid, which was observed by the X-Ray Telescope on board the Hinode satellite on 2007 February 12 (see Animation 2). Observed XRT images are compared with simplified synthetic soft X-ray images from the distribution of the electric currents in the simulation (see Figure 6 and Animation 3). We find that a bright sigmoidal envelope is formed by pairs of J-shaped field lines in the pre-eruptive stage. These field lines form through the BP reconnection and merge later on into S-shaped loops through the tether-cutting reconnection. Both processes can be responsible for the heating of the field lines, and for the formation of small flare loops below the sigmoid. During the eruption, the central part of the sigmoid brightens due to the formation of a vertical current layer in the wake of the erupting flux rope. Slip-running reconnection in this layer yields the formation of flare loops. A rapid decrease of currents due to field line expansion, together with the increase of narrow currents in the reconnecting QSL, yields the sigmoid hooks to thin in the early stages of the eruption. The comparison in Figure 6 shows that this behavior matches the XRT observations of the 2007 February 12 event.

This work has been published in the Astrophysical Journal, see Aulanier et al. (2009), where also the detailed analysis of sigmoids formation and eruption can be found.