CASE 3: TWIST AND WRITHE IN SOLAR ERUPTIONS

Figure 1

Animation 1

Animation 2

Figure 2

Animation 3

Figure 3

Figure 4

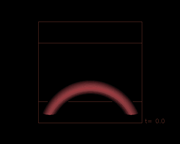
Solar filaments (or prominences) typically display a loop-like shape and signatures of twist when they erupt. Often they also display a helical deformation during their rise, which is often referred to as writhing or kinking, and corresponds to a rotation of the erupting structure about its rise direction (Figure 1). These observational features suggest that erupting filaments are magnetic flux ropes and that, in cases of strong writhing, their eruption is driven by the ideal MHD helical kink instability (KI). Consequently, some filament eruptions have been modelled using kink-unstable flux ropes (see Animation 1). Studying the causes and the amount of writhing in solar eruptions is important, since the magnetic orientation of a CME upon arrival at Earth is one the main factors determining its geoeffectiveness (i.e., the strength of its interaction with the terrestrial magnetosphere).

For a magnetic flux rope, the magnetic helicity is proportional to the sum of its twist and its writhe. The twist measures the number of windings of field lines about the rope axis, whereas the writhe measures the helical deformation of the rope itself. Since helicity is conserved in ideal MHD, twist must be converted in an equal amount of writhe in the course of the KI. Despite the quite frequent occurrence of writhing in erupting filaments, measurements of writhe have been not yet been undertaken, mainly because observations are typically limited to a 2D projection of intrinsically 3D structures onto the plane of the sky. Even for numerical simulations which provide the 3D magnetic field, the temporal evolution of twist and writhe has only extremely rarely been quantified, mainly since the calculation of these quantities based on their general definitions is relatively complicated.

The computation of the writhe is greatly facilitated by its decomposition into local and nonlocal components (Berger and Prior 2006). For kinked flux ropes with one spatial maximum and with both footpoints anchored in the photosphere (as in all examples considered here), the nonlocal writhe measures the rotation of the rope apex out of the plane defined by its footpoints and its apex, whereas the local writhe measures the "internal" helical deformation of the flux rope's two legs. Here we made use of the expressions by Berger and Prior to measure twist and writhe in previously published 3D numerical simulations of flux rope instabilities. Some of the results and their implications for filament eruptions and CMEs are described in the following.

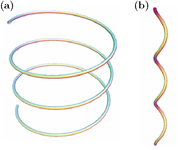
We first measured the evolution of writhe in the 3D MHD simulations of kink-unstable flux ropes by Török et al. (2004). The KI occurs if the flux rope twist exceeds a certain threshold, which is typically 1-2 field line windings from one rope footpoint to the other. Animation 2 shows the evolution of the KI for an initial twist of 2.5 windings. The flux rope is straight in projection initially, so the initial writhe is zero. Since the whole flux rope deforms in the same manner as its axis, the twist converted in the course of the KI can be obtained simply from measuring the writhe along the rope axis.

We found that the amount of converted twist is much smaller (only about 10 per cent of the initial twist, i.e., 0.25 windings for the case shown in Animation 2) than one might intuitively expect from the relatively strong deformation of the flux rope. It is often assumed that the KI converts a twist of one winding, which probably arises from the fact that helical structures on the Sun typically exhibit one helical turn (as the exapmles in Figure 1 and Animation 1), and are therefore often believed to have a writhe of 1 (or -1). However, as the simulation and Figure 2 show, the number of helical turns of a curve or flux rope can be very different from its writhe. It follows that estimations of writhe (and of converted twist) in filament eruptions and CMEs cannot be made from the observed number of turns alone.

We then measured the evolution of writhe in the 3D MHD simulations of confined and ejective flux ropes by Török and Kliem (2005). The simulations are similar to the one shown in Animation 2. The same initial twist of 2.5 windings was used, but now the potential magnetic field overlying the pre-eruptive flux rope was varied. Both simulations could be successfully scaled to fit the morphology and rise characteristics of observed filament eruptions and CMEs. The first simulation (TK1) is shown in Animation 1 above. Here the overlying field was chosen relatively strong, so the rising and kinking flux rope came to a halt at about 3.5 times its initial height, in very good agreement with the observations. Such events, in which the filemant eruption does not yield a CME, are commonly refereed to as confined or failed eruptions. The second simulation (TK2)is shown in Animation 3. It has the same twist as TK1, but an overlying field that drops significantly faster with height. Here the kink-unstable flux rope is additionally accelerated by the ideal MHD torus instability (Kliem and Török 2006), which occurs if the overlying field drops sufficiently fast with height. The additional acceleration yields a full eruption, i.e., a CME is modelled.

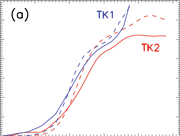
We measured the evolution of the flux rope axis writhe in both simulations (Figure 3). The writhe first grows exponentially, followed by a transition to a saturation phase. The second strong increase in TK1 is caused by an additional deformation of the flux rope axis due to the onset of magnetic reconnection with the overlying field. The nonlocal writhe reaches 0.5 in TK2, corresponding to a rotation of about 90 degrees. A very similar value is found for the rope in TK1 before it starts to reconnect with the overlying field. The temporal evolution of the writhe is very similar in TK1 and TK2, since the growth rate of the KI, largely set by the initial twist, is nearly the same (Figure 3a). The evolution as a function of height, however, is quite different (Figure 3b). The additional acceleration of the rope by the torus instability spreads the rotation of the apex over a larger height range. Given the nearly identical choice of the initial flux rope parameters in the two simulations, one can conclude from Figure 3b that a stronger field immediately above the initial rope does not only resist the evolution into a CME more efficiently, but also produces a more pronounced writhing at low heights.

Since the writhing in CMEs tends to be distributed over a large height range, much of it may escape detection. Typically, the writhing is apparent from the apex rotation of an associated erupting filament or prominence, whose observation is typically limited to the low and middle corona. Therefore, a significant rotation (and the KI) may occur in a larger fraction of CMEs than usually thought. An illustrative example, the filament eruption and CME on 2003 February 18, is shown in Figure 4, together with a comparison of the ejective simulation TK2 shown in Animation 3. The EIT data do not yield indications of a significant rotation, but the Mk4 coronagraph reveals that the legs of the CME core cross to form an "inverse gamma" shape when the core reaches a height of about 1 solar radius above the solar surface. Such a shape develops due to writhing and indicates the occurence of the KI (see also Figure 1 and Animation 1).

This work has been published in Astronomy and Astrophysics. See Török et al. (2010) for more details and further results.